Лягарытм

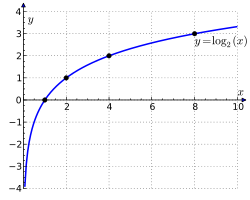
Лягарытм (ад стар.-грэц. λόγος; у перакладзе «слова, сэнс» ды ἀριθμός; у перакладзе «лік») — лік ступені, у які трэба увазьвесьці фіксаваны лік, які называюць базавым, каб ён быў падняты да вытворнага ліку. Напрыклад, лягарытм 1000 па аснове 10 роўны 3, бо 1000 зьяўляецца 10 у ступені 3: 1000 = 10³ = 10 × 10 × 10. Больш агульна, калі x = b^y, то y ёсьць лягарытм х па базе b, што будзе запісана наступным чынам: log_b(x), ці гэтак log₁₀(1000) = 3.

Лягарытм быў уведзены Джонам Нэйпэрам на пачатку XVII стагодзьдзя як сродак для спрашчэньня вылічэньняў. Ён быў хутка прыняты навукоўцамі, інжынэрамі й іншымі для выкананьня вылічэньняў з выкарыстаньнем лягарытмічнай лінейкі й табліцаў лягарытмаў. Гэтыя прылады абапіраюцца на той факт, важны сам па сабе, што лягарытм ёсьць прадукт, які уяўляе сабой суму лягарытмаў множнікаў:

\log _{b}(xy)=\log _{b}(x)+\log _{b}(y).\,

Сучасны панятак лягарытмаў паходзіць ад Леанарда Ойлера, які зьвязаў іх з экспанентамі ў XVIII стагодзьдзі.

Лягарытм з асновай па ліку 10 завецца дзесятковым лягарытмам і мае мноства ужываньняў у галіне навукі й тэхнікі. Натуральны лягарытм мае ў якасьці асновы сталую велічыню е (≈ 2,718), ён шырока выкарыстоўваецца ў чыстай матэматыцы, асабліва вылічэньнях. Двайковы лягарытм выкарыстоўвае лік 2 у якасьці асновы й вядомы ў галіне інфарматыкі.

Лягарытмічныя шкалы паменшаюць шырокія колькасьці меншых абласьцей. Напрыклад, дэцыбэл ёсьць лягарытмічнай адзінкай колькаснага гукавога ціску й напругі. У хіміі, pH і pOH ёсьць лягарытмічнымі мерамі паводле кіслотнасьці воднай рашчыны. Лягарытмы часьцяком сустракаюцца ў навуковых формулах, а таксама пры вымярэньні складанасьці альгарытмаў і геамэтрычных аб’ектаў, званых фракталамі. Яны апісваюць музычныя інтэрвалы, выкарыстоўваюцца ў формулах падліку простых лікаў, паведамляюць некаторыя мадэлі ў псыхафізыцы, а таксама ў судова-бухгальтарскай экспэртызе.

Зьяўляючыся адваротнай функцыяй да ўзьвядзеньня ў ступень, комплексны лягарытм ёсьць інвэрсіўнай функцыяй да экспанэнцыяльнай функцыі, прыкладзенай да камплексных лікаў. Дыскрэтныя лягарытмы знаходзяць прымяненьне ў крыптаграфіі з адчыненым ключом.