Трыкутнік


Трыку́тнік[1][2][3] (тро́хвуго́льнік) у эўклідавай геамэтрыі — тры пункты, якія не ляжаць на адной простай лініі, і тры адцінкі, якія іх злучаюць.
Інакш кажучы, трыкутнік — найпрасьцейшы шматкутнік, які мае 3 вяршыні і 3 бакі.
Вяршыні трыкутніку звычайна пазначаюцца вялікімі лацінскімі літарамі (A, B, C), велічыні кутоў пры адпаведных вяршынях — грэцкімі літарамі (α, β, γ), а даўжыні супрацьлеглых бакоў — маленькімі лацінскімі літарамі (a, b, c).
Трыкутнік зьяўляецца шматграньнікам і 2-сымплексам. У эўклідавай геамэтрыі трыкутнік адназначна задае роўніцу. Усе трыкутнікі двухмерныя.
Клясыфікацыя трыкутнікаў
[рэдагаваць | рэдагаваць крыніцу]| Віды трыкутнікаў паводле велічыні кутоў | ||
|---|---|---|
 Вастракутны |
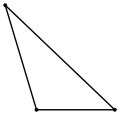 Тупакутны |
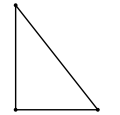 Прастакутны |
Паводле велічыні кутоў
[рэдагаваць | рэдагаваць крыніцу]Паколькі сума кутоў трыкутніку роўная 180°, то ня менш за два куты ў трыкутніку маюць быць вострымі (меншымі за 90°). Вылучаюць наступныя віды трыкутнікаў:
- Калі ўсе куты трыкутніку вострыя, то трыкутнік завецца вастракутным;
- Калі адзін з кутоў трыкутніку тупы (большы за 90°), то трыкутнік завецца тупакутным;
- Калі адзін з кутоў трыкутніку просты (роўны 90°), то трыкутнік завецца прастакутным. Два бакі, што ўтвараюць просты кут, завуцца катэтамі, а бок, супрацьлеглы простаму куту, завецца гіпатэнузай.
| Віды трыкутнікаў паводле колькасьці роўных бакоў | ||
|---|---|---|
 Рознабаковы |
 Раўнаплечы |
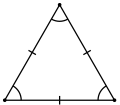 Роўнабаковы |
Паводле колькасьці роўных бакоў
[рэдагаваць | рэдагаваць крыніцу]- Рознабаковым завецца трыкутнік, у якога даўжыні трох бакоў парамі розныя.
- Раўнаплечым завецца трыкутнік, у якога два бакі роўныя. Гэтыя бакі завуцца бочнымі, трэці бок завецца асновай. У раўнаплечым трыкутніку куты пры аснове роўныя. Вышыня, мэдыяна і раўнасечная раўнаплечага трыкутніку, апушчаныя на аснову, супадаюць.
- Роўнабаковым завецца трыкутнік, у якога ўсе тры бакі роўныя. У роўнабаковым трыкутніку ўсе куты роўныя 60°, а цэнтры умежанай і акрэсьленай акружынаў супадаюць.
Няроўнасьць трыкутніку
[рэдагаваць | рэдагаваць крыніцу]Бакі трыкутніку нельга задаваць адвольна, іх зьвязваюць наступныя няроўнасьці
У выпадку выкананьня роўнасьці ў адным зь іх трыкутнік завецца звыродным, далей усюды мяркуецца незвыродны выпадак.
Прыкметы роўнасьці трыкутнікаў
[рэдагаваць | рэдагаваць крыніцу]Трыкутнік адназначна (з дакладнасьцю да кангруэнтнасьці) можна вызначыць па наступных тройках асноўных элемэнтаў:
- a, b, c (роўнасьць паводле трох бакоў);
- a, b, γ (роўнасьць паводле двух бакоў і куту паміж імі);
- a, β, γ (роўнасьць паводле бока і двух прылеглых кутоў).
Адцінкі і акружыны, зьвязаныя з трыкутнікам
[рэдагаваць | рэдагаваць крыніцу]Акружына, датычная ўсіх трох бакоў трыкутніку, завецца яго ўмежанай акружынай. Яна адзіная. Акружына, якая праходзіць праз усё тры вяршыні трыкутніку, завецца яго акрэсьленай акружынай. Акрэсьленая акружына таксама адзіная.
Мэдыянай трыкутніку, праведзенай з дадзенай вяршыні, завецца адцінак, які злучае гэтую вяршыню зь сярэдзінай супрацьлеглага боку. Усе тры мэдыяны трыкутніку перасякаюцца ў адным пункце. Гэты пункт перасячэньня завецца цэнтроідам або цэнтрам цяжару трыкутніку. Апошні назоў зьвязаны з тым, што ў трыкутніку, зробленага з аднастайнага матэрыялу, цэнтар цяжару знаходзіцца ў пункце перасячэньня мэдыянаў. Цэнтроід падзяляе кожную мэдыяну ў стасунку 1:2, калі лічыць ад асновы мэдыяны.
Пэрпэндыкуляр, апушчаны зь вяршыні трыкутніку на супрацьлеглы бок або яго працяг, завецца вышынёй трыкутніку. Тры вышыні трыкутніку перасякаюцца ў адным пункце, які называецца артацэнтрам трыкутніку.
Раўнасечнай трыкутніку, праведзенай з дадзенай вяршыні, завуць адцінак, які злучае гэтую вяршыню з пунктам на супрацьлеглым боку і якая дзеліць кут пры дадзенай вяршыні напалову. Раўнасечныя трыкутніку перасякаюцца ў адным пункце, і гэты пункт супадае з цэнтрам умежанай акружыны.
Як было зазначана, у роўнабаковым трыкутніку раўнасечная, мэдыяна і вышыня, праведзеныя да асновы, супадаюць. Дакладна і зваротнае: калі раўнасечная, мэдыяна і вышыня, праведзеныя з адной вяршыні, супадаюць, то трыкутнік роўнабаковы. Калі трыкутнік рознабаковы, то для любой яго вяршыні раўнасечная, праведзеная зь яе, ляжыць паміж мэдыянай і вышынёй, праведзенымі з той жа вяршыні.
Пасярэднія пэрпэндыкуляры да бакоў трыкутніку таксама перасякаюцца ў адным пункце, які супадае з цэнтрам акрэсьленай акружыны.
Пазаўмежанай акружынай завецца акружына, датычная аднаго боку трыкутніку і працягу двух іншых бакоў.
Сярэдзіны трох бакоў трыкутніку, асновы трох яго вышынь і сярэдзіны трох адцінкаў, якія злучаюць яго вяршыні з артацэнтрам, ляжаць на адной акружыне, якая завецца акружынай дзевяці пунктаў.
У любым трыкутніку цэнтар цяжару, артацэнтар, цэнтар акрэсьленай акружыны і цэнтар акружыны дзевяці пунктаў ляжаць на адной простай лініяй, якая называецца простай Ойлера.
Суадносіны ў трыкутніку
[рэдагаваць | рэдагаваць крыніцу]Калі вядомыя тры велічыні, паказаныя вышэй, то астатнія можна знайсьці па наступных формулах:
(З тэарэмы выцякае, што калі a < b < c, то α < β < γ)
- c² = a² + b² — 2ab cos γ
(Зьяўляецца абагульненьнем тэарэмы Пітагора)
- α + β + γ = 180° (π)
Іншыя суадносіны
[рэдагаваць | рэдагаваць крыніцу]Мэтрычныя суадносіны ў трыкутніку прыведзеныя для трыкутніку :
Дзе:
— адпаведна раўнасечныя кутоў , і ,
— адцінкі, на якія раўнасечная дзеліць бок ,
— мэдыяны, праведзеныя адпаведна да бакоў , і ,
— вышыні, апушчаныя адпаведна на бакі , і ,
— радыюс умежанай акружынай,
— радыюс акрэсьленай акружынай,
— напаўпэрымэтар,
— плошча,
— адлегласьць паміж цэнтрамі ўмежанай і акрэсьленай акружынаў.
Плошча трыкутніку
[рэдагаваць | рэдагаваць крыніцу]Найвядомейшая й найпрасьцейшая формула:
Дзе:
— даўжыня асновы трыкутніку (бок, на які праведзены пэрпэндыкуляр)
— вышыня, праведзеная на бок ,
Гэтая формула можа быць выкарыстана толькі тады, калі можна лёгка знайсьці вышыню.

Трыганамэтрычны спосаб
[рэдагаваць | рэдагаваць крыніцу]Вышыню трыкутніку можна вызначыць з выкарыстаньнем трыганамэтрычных формулаў. У адпаведнасьці з пазначэньнямі на выяве леваруч, вышыня роўная . Калі падставіць вышыню ў формулу якая прыведзеная вышэй, атрымаем:
Апроч гэтага, , што справядліва і для іншых двух кутоў:
З выкарыстаньнем вэктараў
[рэдагаваць | рэдагаваць крыніцу]Плошчу паралелаграма можна вылічыць з дапамогай вэктараў. Няхай вэктары AB і AC спраставаны адпаведна ад A да B і ад A да C. Тады плошча паралелаграма ABDC роўная |AB × AC|, г.зн. лічбаваму значэньню вэктарнаму множаньню AB і AC. |AB × AC| роўнае |h × AC|, дзе h — вышыня паралелаграма як вэктар.
Плошча трыкутніку ABC роўная палове плошчы паралелаграма S = ½|AB × AC|.
Плошчу трыкутніку ABC таксама можна вылічыць як скалярнае множаньне вэктараў.
Выкарыстаньне каардынатаў
[рэдагаваць | рэдагаваць крыніцу]Калі пункт А разьмешчаны ў пункце адліку (0, 0) Дэкартавай каардынатнай сыстэмы, а каардынаты іншых двух пунктаў B = (xB, yB) і C = (xC, yC), тады плошча S можа быць вылічана як ½ абсалютнага значэньня дэтэрмінанту:
У больш агульным выпадку:
У трохмернай прасторы плошча трыкутніку {A = (xA, yA, zA), B = (xB, yB, zB) і C = (xC, yC, zC)} роўная Пітагоравае суме адпаведных праекцыяў на тры галоўныя роўніцы (для якіх x = 0 або y = 0 або z = 0):
Формула Герона
[рэдагаваць | рэдагаваць крыніцу]Форма трыкутніку адназначна вызначаецца трыма бакамі. Адпаведна, для таго каб падлічыць плошчу дастаткова ведаць даўжыню бакоў. Паводле формулы Герона:
де s = ½ (a + b + c) — напаўпэрымэтар
Іншы спосаб запісу формулы Герона:
Іншыя формулы
[рэдагаваць | рэдагаваць крыніцу]- у дадзенай формуле варта зьвярнуць увагу на абыход вяршыняў, калі ісьці паводле гадзіньнікавай стрэлцы, то атрымаецца тая ж плошча, але з адмоўным знакам
- — для прастакутнага трыкутніку
Дзе:
— напаўпэрымэтар,
— радыюс умежанае акружыны,
— радыюс пазаўмежанае акружыны, датычны боку ,
— радыюс акрэсьленае акружыны,
— каардынаты вяршыняў трыкутніку.
Глядзіце таксама
[рэдагаваць | рэдагаваць крыніцу]- Тэарэма пра суму кутоў трыкутніку
- Тэарэма сынусаў
- Тэарэма косынусаў
- Формула Герона
- Выбітныя пункты трыкутніку
- Сярэдняя лінія трыкутніку
Крыніцы
[рэдагаваць | рэдагаваць крыніцу]- ^ Тэрміналагічны слоўнік па вышэйшай матэматыцы для ВНУ / Т. Сухая, Р. Еўдакімава, В. Траццякевіч, Н. Гудзень. — Мн.: Навука і тэхніка, 1993. С. 81, 160
- ^ Трыкутнік // Беларуска-расійскі слоўнік / Укладальнікі: М. Байкоў, С. Некрашэвіч. — Менск: Дзяржаўнае выдавецтва Беларусі, 1925. Факсімільнае выданьне: Менск: Народная асвета, 1993. ISBN 5-341-00918-5
- ^ Руска-беларускі фізічны слоўнік / Уклад. Самайлюковіч У., Пазняк У., Сабалеўскі А. — Мн.: Навука і тэхніка, 1994. С. 250














































![{\displaystyle S_{\triangle ABC}={\frac {1}{2}}[x_{A}(y_{B}-y_{C})+x_{B}(y_{C}-y_{A})+x_{C}(y_{A}-y_{B})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99ee12bb827ad2b6bea64e8f48142d47aa0ac1a6)


