Экспанэнтавая натацыя

Экспанэ́нтавая ната́цыя, навуко́вы за́піс — спосаб запісу лікаў, надта вялікіх ці вельмі маленькіх для зручнага запісу ў дзесятковай форме. Такую заснаваную на дзесятковай базе натацыю шырока ўжываюць навукоўцы, матэматыкі ды інжынэры, бо яна дазваляе спрасьціць арытмэтычныя апэрацыі.

Дзесятковы запіс	Навуковы запіс
2	2×10⁰
300	3×10²
4321.768	4.321768×10³
−53000	−5.3×10⁴
6720000000	6.72×10⁹
02	2×10⁻¹
987	9.87×10²
0.00000000751	7.51×10⁻⁹

У экспанэнтавай натацыі ненулявыя лікі запісваюць у форме

m × 10ⁿ

альбо m, памножанае на дзесяць у ступені n, дзе n — цэлы лік, а каэфіцыент m — ненулявы рэчаісны лік (звычайна паміж 1 і 10 у модулі, і запісаны найчасьцей зь дзесятковым разьдзяляльнікам). Цэлы лік n называецца экспанэнтай, а рэчаісны m — вартасным лікам(d) або мантысай^[1]. Калі лік адмоўны, то перад m дадаецца сымбаль мінусу, як і ў звычайнай дзесятковай натацыі. У нармалізаванай натацыі экспанэнту выбіраюць так, каб абсалютная велічыня (модуль) вартаснага ліку m была ня меншай за 1 і меншай за 10.

Нармалізаваная натацыя

Любы рэчаісны лік можна запісаць формулай m×10^ⁿ рознымі спосабамі: напрыклад, 350 можна запісаць як 3.5×10², 35×10¹ або 350×10⁰.

У нармалізаваным навуковым запісе экспанэнту n выбіраюць такім чынам, каб абсалютная велічыня m была ня меншай за адзінку, але меншай за дзесяць (1 ≤ |m| < 10). Такім чынам, 350 варта запісаць у выглядзе 3.5×10². Такая форма дазваляе лягчэй параўноўваць лікі: лікі з большымі экспанэнтамі (дзякуючы нармалізацыі) будуць большымі, чым лікі зь меншымі экспанэнтамі, а адніманьнем экспанэнтаў можна ацаніць парадак велічыні(d), на які адрозьніваюцца лікі. Для лікаў з абсалютным значэньнем між 0 і 1 экспанэнта n у нармалізаванай натацыі адмоўная (то бок 0,5 запісваецца ў выглядзе 5×10⁻¹). Калі экспанэнта роўная 0, то экспанэнтную частку ліку (уключаючы 10) можна абмінуць. Пры патрэбе складаньня ці адыманьня (або якога-кольвек іншага параўнаньня) некалькіх лікаў зручна для ўсіх элемэнтаў выкарыстоўваць аднолькавае значэньне m.

Нармалізаваны навуковы запіс — тыповая форма запісу вялікіх нумароў у мностве навуковых галінаў. Часта яго называюць проста экспанэнцыйнай натацыяй — хоць гэты тэрмін больш агульны і ўключае таксама выпадкаў, дзе m не абмежаваны дыяпазонам ад 1 да 10, а базы(d) могуць быць ня толькі 10 (напрыклад, 3,15×2^²⁰).

Інжынэрная натацыя

Інжынэрная натацыя адрозьніваецца ад нармалізаванай навуковай натацыі тым, што экспанэнта n абмежаваная ступенямі(d) тройкі. Адпаведна абсалютнае значэньне мантысы m можа прымаць значэньні 1 ≤ |m| < 1000, а не 1 ≤ |m| < 10. Інжынэрная натацыя дазваляе запісваць нумары адпаведна іхнім прыстаўкам СІ, напрыклад 12.5×10⁻⁹ м можна прачытаць як «12 з паловай нанамэтраў» і запісаць як 12.5 нм, а пры запісе ў навуковай натацыі 1.25×10⁻⁸ м давялося б называць гэты лік «адна цэлая дваццаць пяць сотых памножанае на дзесяць у мінус восьмай ступені мэтраў».

Вартасныя лічбы

Вартасная лічба(d) — гэта разрад у ліку, які падвышае ягоную дакладнасьць. Сюды ўключаюцца ненулявыя лікі, нулі між вартаснымі лічбамі і нулі, якія пакінутыя дзеля пазначэньня вартасьці. Вядучыя і канечныя нулі ня лічацца вартаснымі разрадамі, бо патрэбныя толькі для паказу парадку ліку. На жаль, гэта прыводзіць да неадназначнасьцяў. Звычайна лічаць, што лік 1230400 мае пяць вартасных лічбаў: 1, 2, 3, 0 і 4, а два апошнія нулі ёсьць толькі структурнымі сымбалямі, якія не павялічваюць дакладнасьць. Аднак нават у тым выпадку, калі пры вымярэньнях два апошнія разрады былі вымераныя дакладна і аказаліся роўнымі нулю, лік усё адно быў бы запісаны ў такім самым выглядзе зь сям’ю вартаснымі лічбамі.

Пры пераводзе такога ліку ў нармалізаваны навуковы запіс ён дзеліцца да мантысы паміж 1 і 10. Усе вартасныя лічбы захоўваюцца, а канечныя нулі адкідаюцца. Такім чынам, лік 1230400 стане 1.2304×10⁶, як бы меў пяць вартасных разрадаў. Калі б лік меў шэсьць або сем вартасных разрадаў, дык быў запісаны б як 1.23040×10⁶ або 1.230400×10⁶. Такім чынам, яшчэ адной перавагай навуковага запісу ёсьць адназначная колькасьць вартасных разрадаў.

Натацыя «E»

Дысплэй калькулятара Texas Instruments TI-84 Plus з вывадам канстанты Авагадра ў запісе E

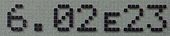
Большасьць калькулятараў і шматлікія кампутарныя праграмы выводзяць вельмі вялікія і малыя вынікі ў навуковым запісе, які ў розных вытворцаў і мадэлях уключаецца клявішай з надпісам EXP (то бок exponent), EEX (то бок enter exponent), EE, EX, E або ×10^x. Паколькі ня ўсе зь іх могуць правільна выводзіць надрадковыя сымбалі накшталт 10⁷, для аддзяленьня «дзясяткі ў ступені» выкарыстоўваецца літара E або e (што можна запісаць як „× 10ⁿ“), пасьля чаго ідзе значэньне экспанэнты; інакш кажучы, для любога рэчаіснага ліку m і цэлага n вывад «mEn» будзе азначаць значэньне m × 10ⁿ. У гэтым выпадку сымбаль e ня тычыцца ані канстанты e, ані паказьнікавай функцыі e^x. Выкарыстаньне натацыі «E» палягчае ўвод інфармацыі і чытэльнасьць у тэксьце, бо зьмяншае колькасьць націскаў клявішаў, дапамагае ўнікнуць выкарыстаньня дробных шрыфтоў ды стварае прасьцейшы і выразьнейшы вывад.

Тыпаграфіка

У нармалізаваным навуковым запісе, у інжынэрнай і натацыі «E» пропуст дазваляецца толькі перад і пасьля «×» альбо перад «E» і часам апускаецца.

Прыклады навуковага запісу

Маса электрона прыкладна роўная 0.000000000000000000000000000000910938356 кг^[2]. У навуковым запісе гэта выражаецца так: 9.10938356×10⁻³¹ кг (у адзінках СІ).
Маса Зямлі прыкладна роўная 5972400000000000000000000 кг^[3]. У навуковым запісе гэта выражаецца так: 5.9724×10²⁴ кг.
Даўжыня акружыны Зямлі прыкладна роўная 40000000 м^[4]. У навуковым запісе гэта выражаецца так: 4×10⁷ м. У інжынэрным запісе гэта выражаецца так: 40×10⁶ м. У сыстэме СІ гэта можна запісаць так: 40 Мм (40 мэгамэтраў).

Перавод лікаў

У дадзеным выпадку разглядаем перавод лікаў зь дзесятковай сыстэмы ў навуковы запіс, назад у дзесятковую форму альбо зьмяненьне экспанэнцыйнай часткі выразы. Сам лік пры гэтым не зьмяняецца, зьмяняецца толькі ягонае адлюстраваньне.

Зь дзесятковай у навуковую

Сьпярша трэба перамясьціць коску разьдзяляльніка цэлай і дробнай частак на n пазыцыяў, каб значэньне цэлай часткі было ня менш за 1, але менш за 10. Калі разьдзяляльнік пры гэтым зьмяшчаўся ўлева, трэба дадаць × 10ⁿ; калі ж управа — тады × 10⁻ⁿ. Каб прадставіць лік 1,230,400 у нармальным навуковым запісе, коску варта перамясьціць на 6 разрадаў улева і дадаць × 10⁶; атрымаем 1.2304×10⁶. У ліку −0.0040321 варта перамясьціць коску на 3 разрады ўправа, а ня ўлева, што дасьць вынік −4.0321×10⁻³.

З навуковай у дзесятковую

Каб перавесьці лік з навуковага запісу ў дзесятковы, сьпярша трэба пазбавіцца канчатку × 10ⁿ, пасьля чаго перанесьці дзесятковую коску на n разрадаў управа (калі n дадатны) або ўлева (калі n адмоўны). Прыкладам, у ліку 1.2304×10⁶ варта зьмясьціць коску на 6 разрадаў управа; атрымаем 1,230,400. У ліку −4.0321×10⁻³ варта зьмясьціць коску на 3 разрады ўлева; атрымаем −0.0040321.

Экспанэнцыйная

Перавод між рознымі навуковымі спосабамі запісу з рознымі значэньнямі экспанэнты атрымліваецца правядзеньнем апэрацый множаньня або дзяленьня на ступень дзясяткі над мантысай і адыманьнем або складаньнем экспанэнты адпаведна. Дзесятковая коска ў мантысе пераносіцца на x улева (ці ўправа), а да экспанэнты дадаецца (або адымаецца ад яе) x, як паказана ніжэй.

1.234×10³ = 12.34×10² = 123.4×10¹ = 1234

Асноўныя апэрацыі

Маем два лікі ў навуковай натацыі,

$x_{0}=m_{0}\times 10^{n_{0}}$ і $x_{1}=m_{1}\times 10^{n_{1}}$

Множаньне і дзяленьне выконваюцца па правілах апэрацый ступеняваньня:

$x_{0}x_{1}=m_{0}m_{1}\times 10^{n_{0}+n_{1}}$ і ${\frac {x_{0}}{x_{1}}}={\frac {m_{0}}{m_{1}}}\times 10^{n_{0}-n_{1}}$

Колькі прыкладаў: $5.67\times 10^{-5}\times 2.34\times 10^{2}\approx 13.3\times 10^{-5+2}=13.3\times 10^{-3}=1.33\times 10^{-2}$ і ${\frac {2.34\times 10^{2}}{5.67\times 10^{-5}}}\approx 0.413\times 10^{2-(-5)}=0.413\times 10^{7}=4.13\times 10^{6}$

Для складаньня і адыманьня неабходна прывесьці лікі да аднолькавай экспанэнтнай часткі, тады мантысы можна проста скласьці або адняць:

x_{0}=m_{0}\times 10^{n_{0}}

і

x_{1}=m_{1}\times 10^{n_{1}}

дзе

n_{0}=n_{1}

Пасьля гэтага складзіце ці адыміце экспанэнты: $x_{0}\pm x_{1}=(m_{0}\pm m_{1})\times 10^{n_{0}}$

Прыклад: $2.34\times 10^{-5}+5.67\times 10^{-6}=2.34\times 10^{-5}+0.567\times 10^{-5}=2.907\times 10^{-5}$

Іншыя базісы

Звычайна для навуковай натацыі выкарыстоўваюцца ступені дзясяткі, аднак могуць ужывацца й ступені іншых лікаў, найчасьцей двойкі.

Напрыклад, у навуковым запісе з базісам 2 лік 1001₂ у двайковай сыстэме (=9₁₀) запісваецца як 1.001₂ × 2₁₀^11₂ альбо 1.001₂ × 10₂^11₂ з выкарыстаньнем двайковых лічбаў (альбо карацей 1.001 × 10¹¹). У запісе «E» гэта запісваецца як 1.001₂E11₂ (альбо карацей 1.001E11), дзе літара E цяпер азначае «двойка (10₂) у ступені». Дзеля лепшага адрозьненьня экспанэнты ў базісе 2 ад экспанэнты ў базісе 10 першы часам пазначаюць літарай B замест E, як у 1.001₂B11₂ (альбо карацей 1.001B11). Для параўнаньня той самы лік у дзесятковым прадстаўленьні(d): 1.125 × 2³ альбо 1.125B3. Некаторыя калькулятары маюць зьмяшаную форму прадстаўленьня двайковых лікаў з плаваючай коскай, дзе экспанэнта выводзіцца ў дзесятковай сыстэме нават у двайковым рэжыме; такім чынам, вышэйшы прыклад выглядацьме так: 1.001₂ × 10₂^3₁₀, альбо скарочана 1.001B3^[5].

Падобна да B, літарамі H^[5] і O^[5] часам пазначаюць ступені лікаў 16 альбо 8 адпаведна, напрыклад 1.25 = 1.40₁₆ × 10₁₆^0₁₆ = 1.40H0 = 1.40h0, альбо 98000 = 2.7732₈ × 10₈^5₈^[5].

Інжынэрную натацыю(d) можна разглядаць як навуковую з базісам 1000.

Глядзіце таксама

Крыніцы

^ Franca Caliò, Alessandro Lazzari. Elements of Mathematics with Numerical Applications. — Società Editrice Esculapio, 2017. — С. 30–32. — ISBN 978-8-89385052-0
^ Peter J. Mohr, David B. Newell, Barry N. Taylor CODATA recommended values of the fundamental physical constants: 2014 // Reviews of Modern Physics. — July–September 2016. — В. 3. — Т. 88. — С. 035009. — DOI:10.1103/RevModPhys.88.035009
^ Brian Luzum, Nicole Capitaine, Agnès Fienga, William Folkner, Toshio Fukushima, James Hilton, Catherine Hohenkerk, George Krasinsky, Gérard Petit, Elena Pitjeva, Michael Soffel, Patrick Wallace. The IAU 2009 system of astronomical constants: The report of the IAU working group on numerical standards for Fundamental Astronomy // Celestial Mechanics and Dynamical Astronomy. — August 2011. — В. 4. — Т. 110. — С. 293–304. — DOI:10.1007/s10569-011-9352-4
^ Various Handbook of Chemistry and Physics / David R. Lide. — 81st. — CRC, 2000. — ISBN 978-0-8493-0481-1
^ ^а ^б ^в ^г Schwartz Jake, Rick Grevelle. HP16C Emulator Library for the HP48S/SX. — 1. — 2003.

Вонкавыя спасылкі

[Calio_2017-1] Franca Caliò, Alessandro Lazzari. Elements of Mathematics with Numerical Applications. — Società Editrice Esculapio, 2017. — С. 30–32. — ISBN 978-8-89385052-0

[CODATA2014Full-2] Peter J. Mohr, David B. Newell, Barry N. Taylor CODATA recommended values of the fundamental physical constants: 2014 // Reviews of Modern Physics. — July–September 2016. — В. 3. — Т. 88. — С. 035009. — DOI:10.1103/RevModPhys.88.035009

[Luzum_2011-3] Brian Luzum, Nicole Capitaine, Agnès Fienga, William Folkner, Toshio Fukushima, James Hilton, Catherine Hohenkerk, George Krasinsky, Gérard Petit, Elena Pitjeva, Michael Soffel, Patrick Wallace. The IAU 2009 system of astronomical constants: The report of the IAU working group on numerical standards for Fundamental Astronomy // Celestial Mechanics and Dynamical Astronomy. — August 2011. — В. 4. — Т. 110. — С. 293–304. — DOI:10.1007/s10569-011-9352-4

[Lide_2000-4] Various Handbook of Chemistry and Physics / David R. Lide. — 81st. — CRC, 2000. — ISBN 978-0-8493-0481-1

[HP16C-Lib-5] а ^б ^в ^г Schwartz Jake, Rick Grevelle. HP16C Emulator Library for the HP48S/SX. — 1. — 2003.

[1]

[2]

[3]

[4]

[5]